In this article, I will explain linear and non-linear vibrations in an easy-to-understand, non-mathematical way and then I will relate these concepts to machinery vibration monitoring.

Linear Systems

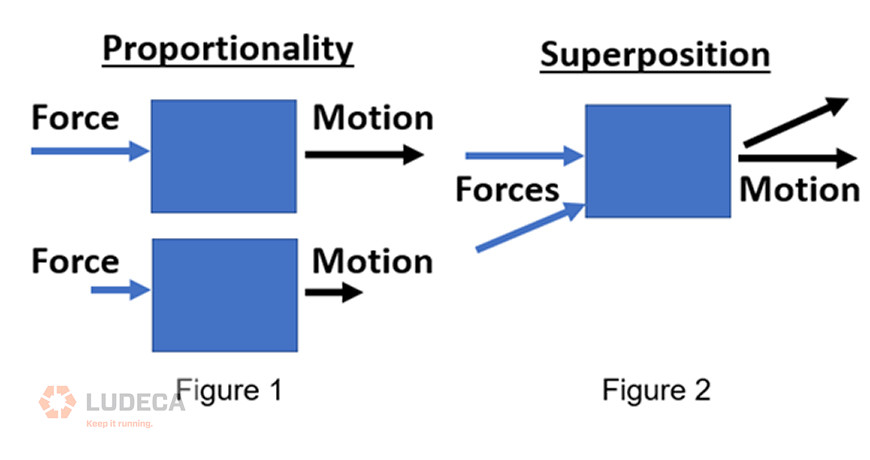
The definition of a linear system is that the output is directly proportional to the input. If you hit a billiard ball in one direction, it will move in that direction. If you hit it harder, it will move farther. This is a property called “proportionality”. (Figure 1)

If you hit the ball in two directions simultaneously, it will move in a combination of those two. This property is called “superposition.” (Figure 2)

Non-Linear Systems

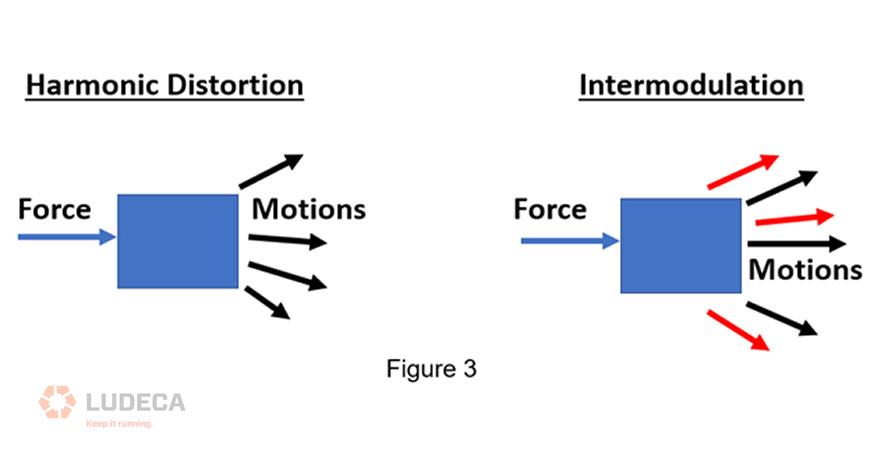
A non-linear system will contain things in the output that were not contained in the input. Rather than hitting a billiard ball, imagine hitting a cube of gelatin. You hit in one direction, but it wiggles in various directions. It moves in a number of ways that were not included in the input and are not proportional to the input. These nonlinear responses include the principles of harmonic distortion and intermodulation. (Figure 3)

Linear Machine Vibration

In a rotating machine, we can take the force generated by an unbalance mass on the rotor as the forcing frequency being input into the system. The unbalance mass rotates around with the shaft and generates a force (F) equal to the mass (m) times the radius (r) of the mass from the center of rotation times the running speed (w) squared.

F = mrw²

We can define this input force as a sine wave. If we did the FFT of this sine wave, we would get a single peak in the vibration spectrum at the shaft rotational rate. Anyone who has monitored machinery vibration will know however that in real life, not only do we see a peak at the shaft rotation rate, we also see harmonics (or multiples) of this frequency in the vibration spectrum.

Harmonics Are Examples of Non-Linearities

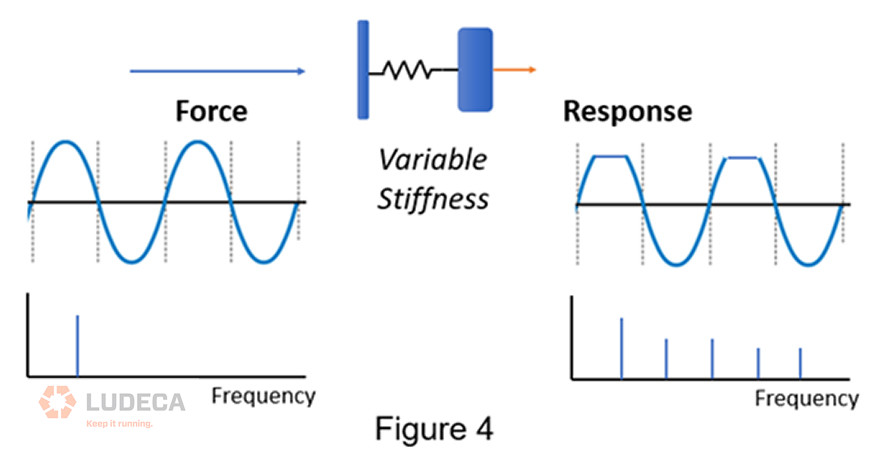
Why do we see harmonics of running speed? Because the machine is not a perfectly linear system. Here is a simple way to understand what is happening. Imagine the unbalance force is being input into a spring mass system with a stiffness (k). If the spring mass system is “linear” we can define it with the equation F=kx, where F is the input force and x is the displacement of the mass (or its vibration in units of displacement). This is a linear equation in that if “F” goes up, “x” goes up proportionally and if F goes down, x also goes down proportionally.

Now imagine that as you compress the spring, it gets stiffer. In other words, k changes or varies with displacement x. You could also imagine that the spring gets less stiff the more you stretch it. I won’t write this down as a mathematical equation, but the fact that k varies with x makes this a non-linear equation. F and X will no longer always be directly or linearly proportional because k is also varying. If the input is a sine wave, the output is going to be a distorted sine wave – either flatter where the system increases in stiffness or taller where stiffness decreases. When we do the FFT of this distorted wave, we get harmonics in the spectrum. This is a non-linear response because these new harmonic frequencies were not in the input but they are in the output! (Figure 4)

Sidebands Are Also the Result of Non-linearities

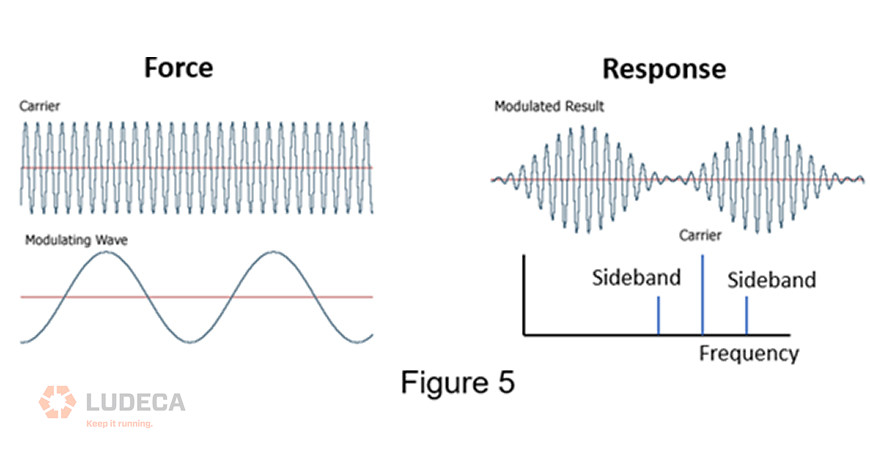
Amplitude (or frequency) modulation in the time waveform results in sidebands in the spectrum. Amplitude modulation is the repetitive change (modulation) in the amplitude of a signal (the carrier). Although the input only contains a single frequency (the carrier) that is varying in amplitude at a certain rate, the output contains the carrier frequency plus and minus the modulating frequency. These peaks on either side are called sidebands. This is a nonlinear response because there is nothing in the input that is actually happening at the sideband frequencies. These are new. (Figure 5)

Amplitude modulation and sidebands are common in rolling element bearing defects, electric motors, and gears. We can say in a general way that as a defect worsens over time we will expect to see more (quantity) and higher amplitude harmonics and sidebands.

How Does This Relate to Machine Health?

In a general sense, we can say that healthy machines behave in a more linear fashion than unhealthy machines. Defects such as cracks, loose bolts, rotating looseness, and rubs will result in non-linear behavior and we will see more and larger harmonics in the vibration spectrum. In the case of journal-bearing rubs or looseness; we may even see a pattern of subharmonics. These are sub multiples of running speed (1/2 x, 1/3 x, or even 1/4 x harmonics.) You can think of a rub as an increase in stiffness and looseness as a lessening of stiffness.

In a general, qualitative way, we can say that a healthy machine will have a “cleaner” spectrum and as the machine wears out or becomes defective, we will see more and larger harmonics, sidebands, and noise.

Want to Learn More?

Alan Friedman dba Zenco offers machinery vibration analysis courses and certification in accordance with ISO 18436-2. You can see the live course schedule here: www.ZencoVibrations.com/events You can connect with him on Linkedin. In addition to public classroom training and public virtual courses, Alan is also available for private courses virtually or on-site in addition to informal training and mentoring. Category I and II vibration are also available in Spanish.

Alan, aka the Vibe Guru, has over 30 years of vibration analysis experience, He has trained thousands of students around the world up to Category IV. One of the things that makes Alan a great teacher is his ability to teach people where they are at. Whether you are a math-challenged millwright, an engineer, or a PhD, Alan will challenge you without overwhelming you. If you are interested in condition monitoring you can also check out his book: Audit It. Improve It! Getting the Most from your Vibration Monitoring Program or hire him for an on-site program audit.

Did you know that Alan Friedman left Mobius and is now providing his own courses?